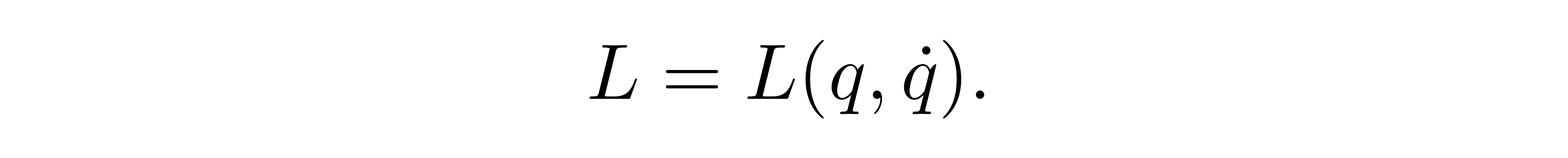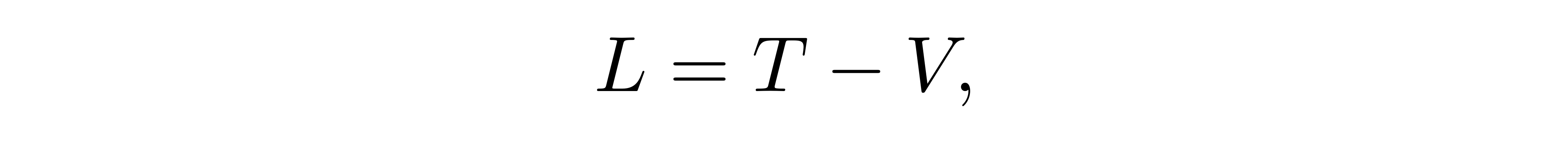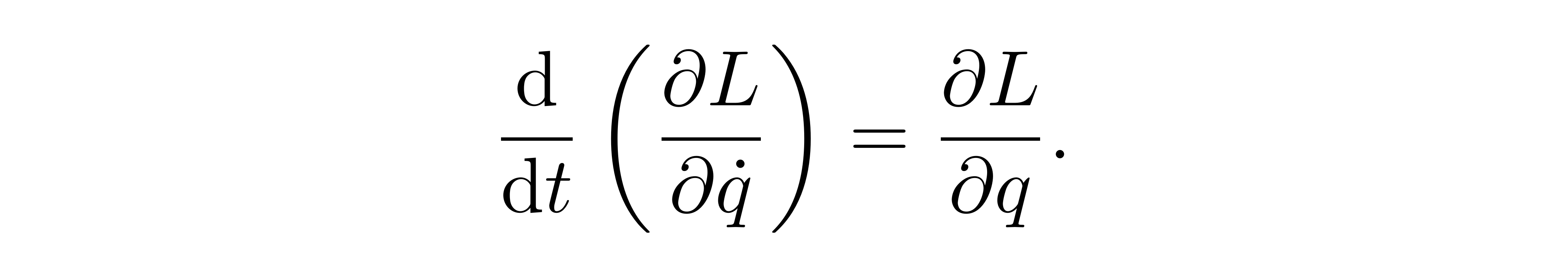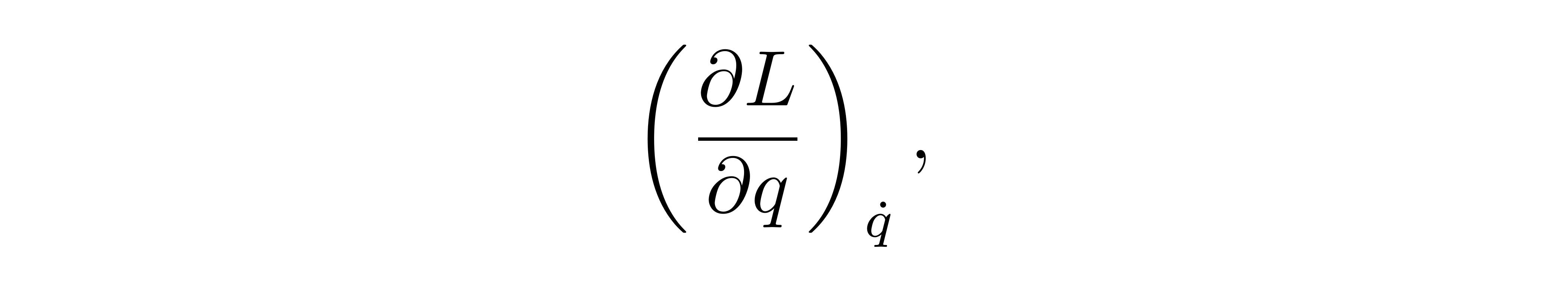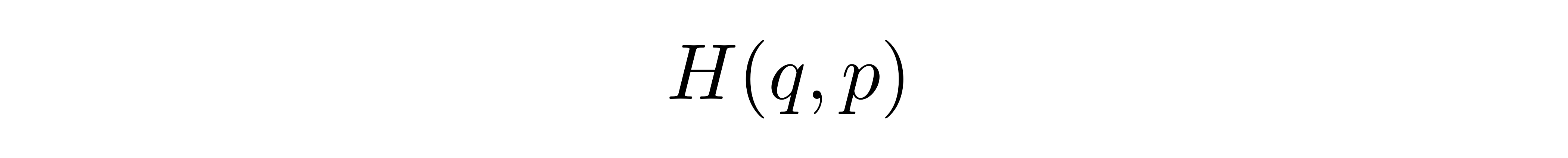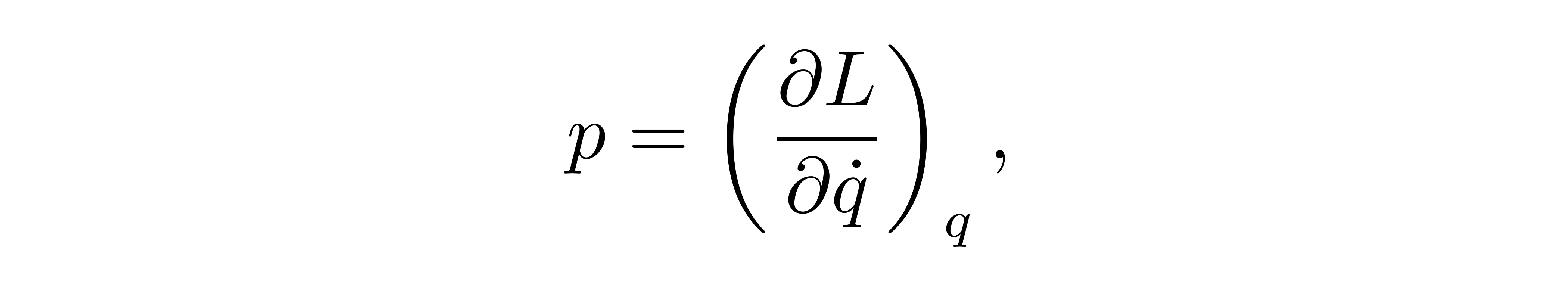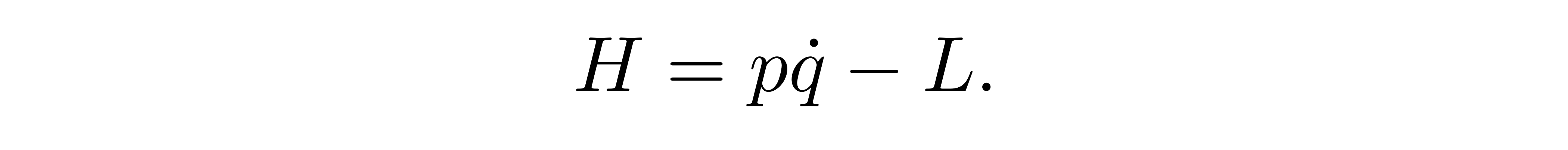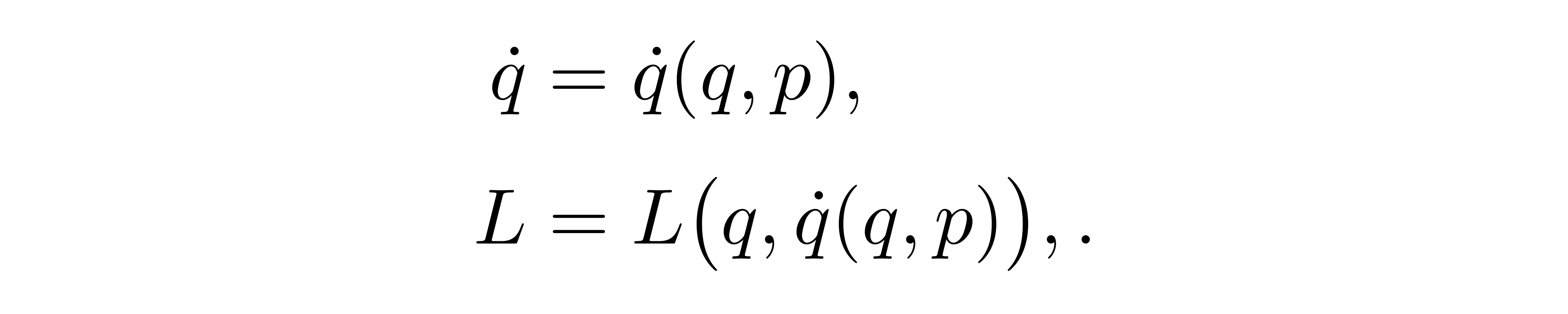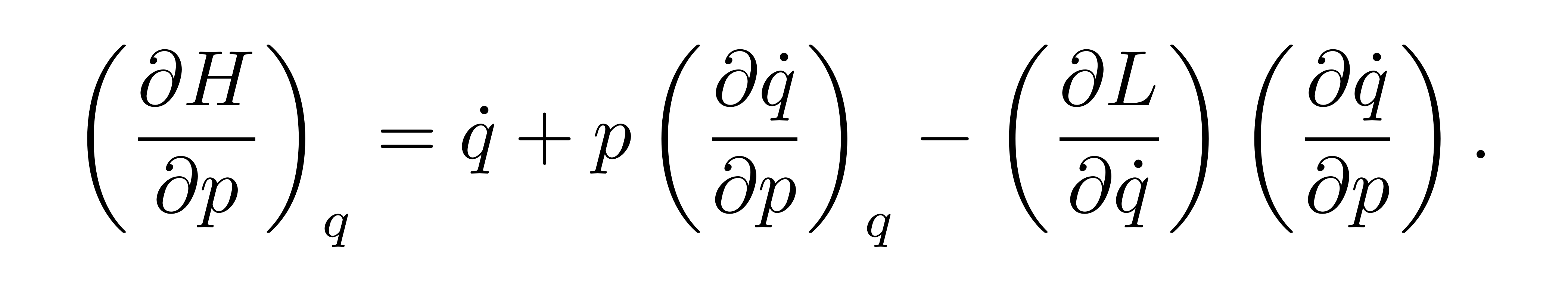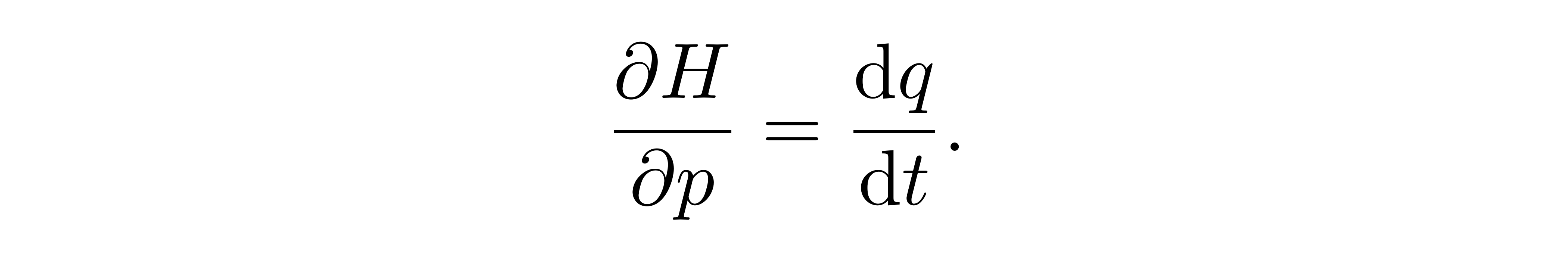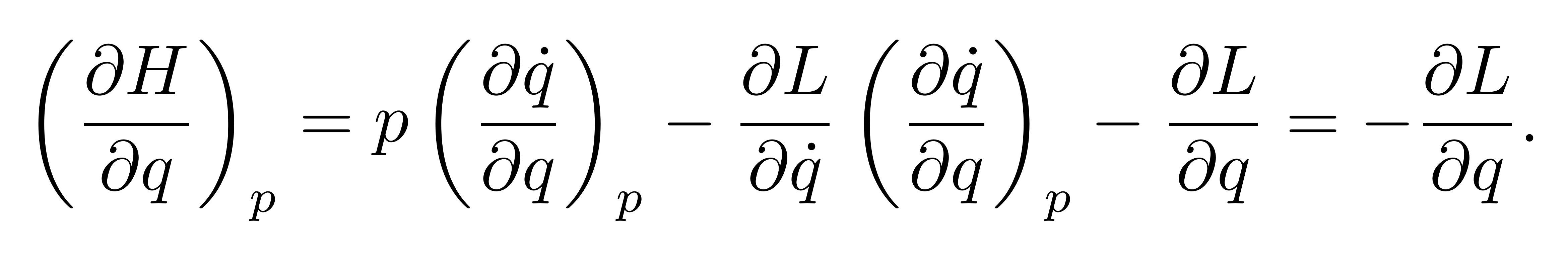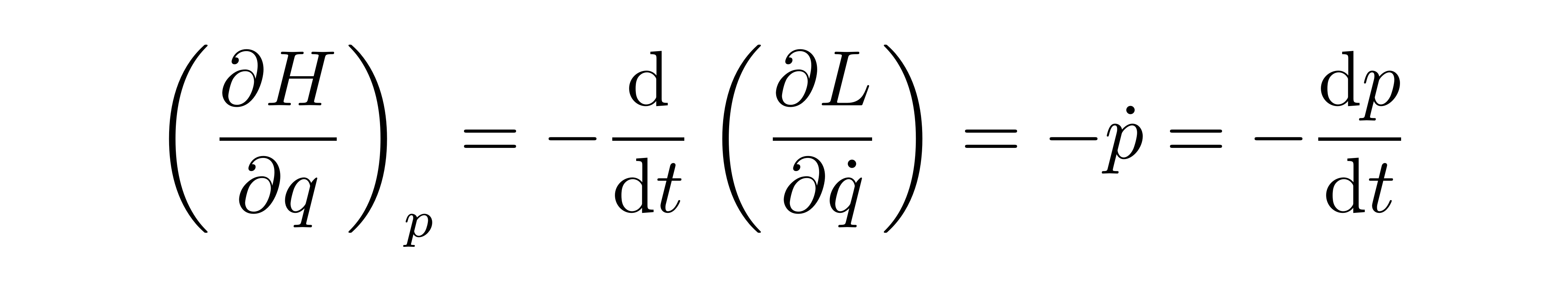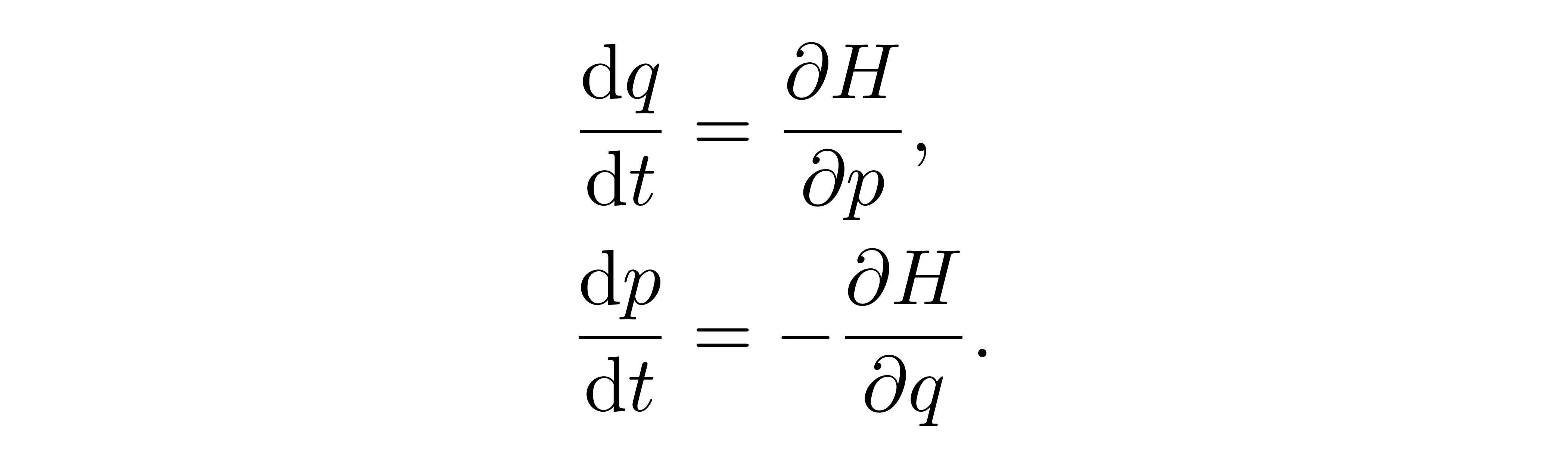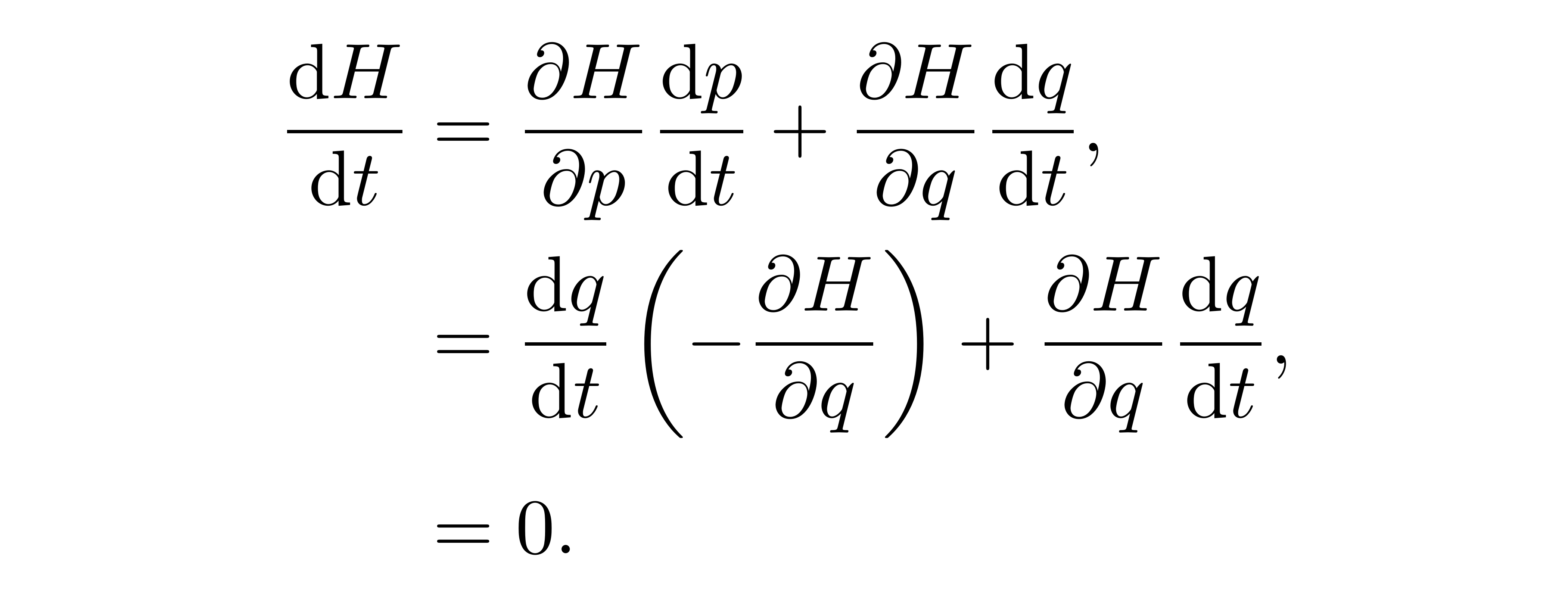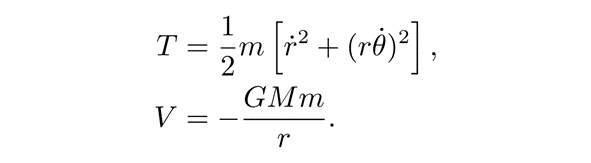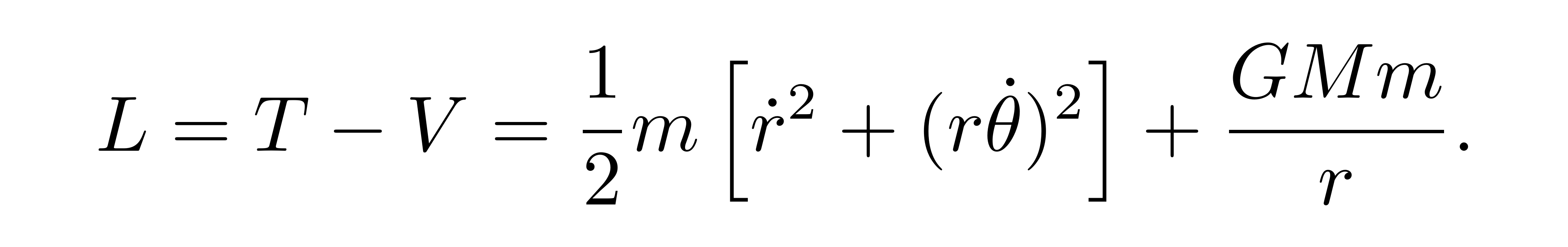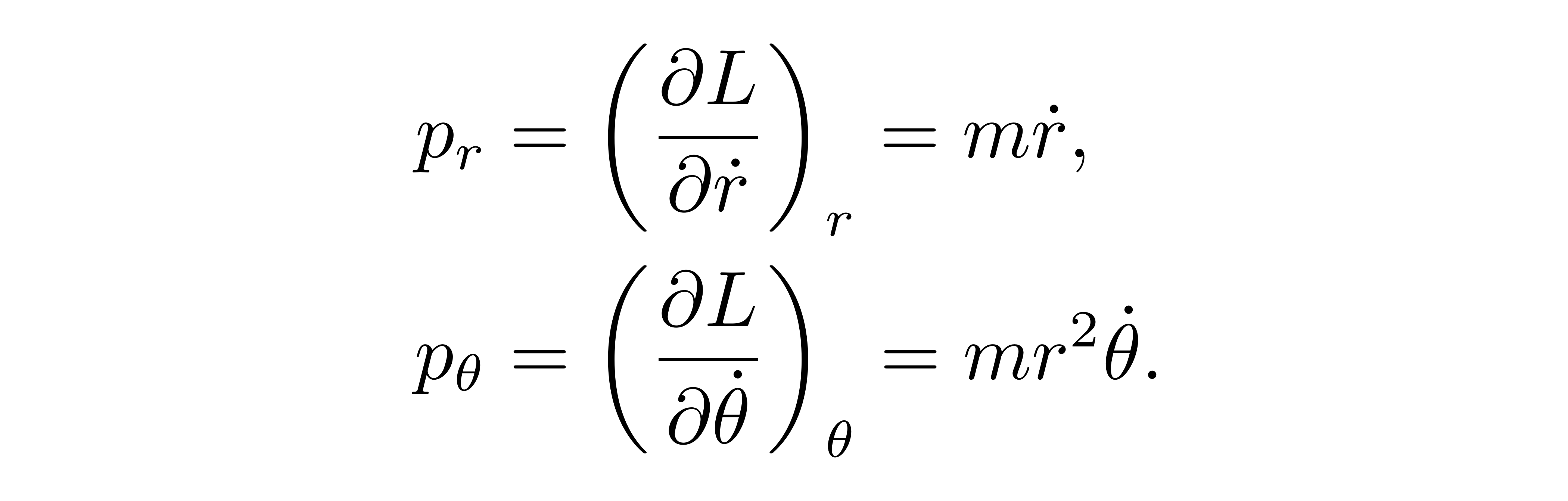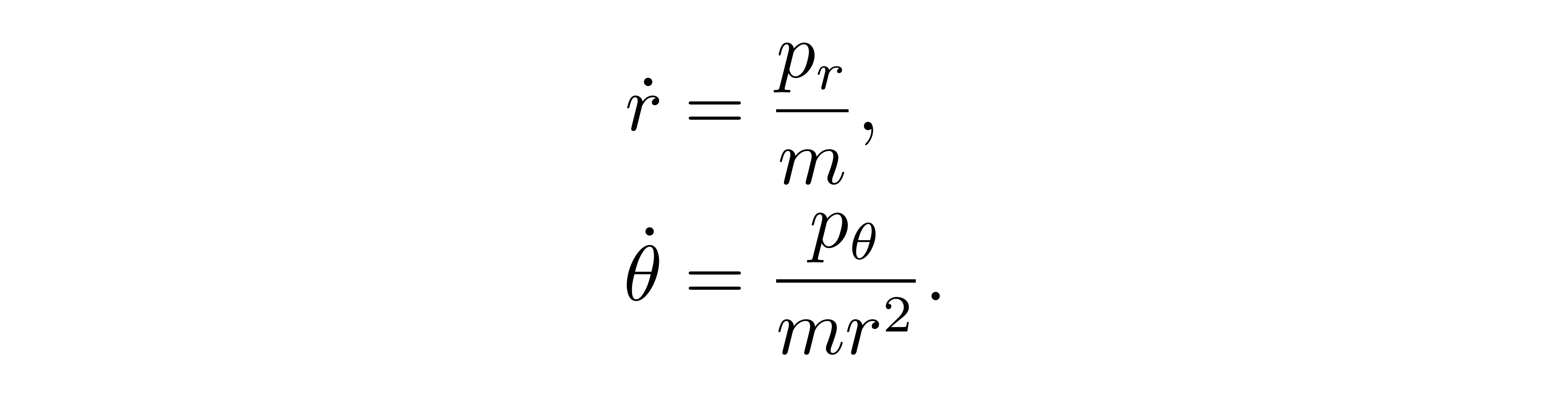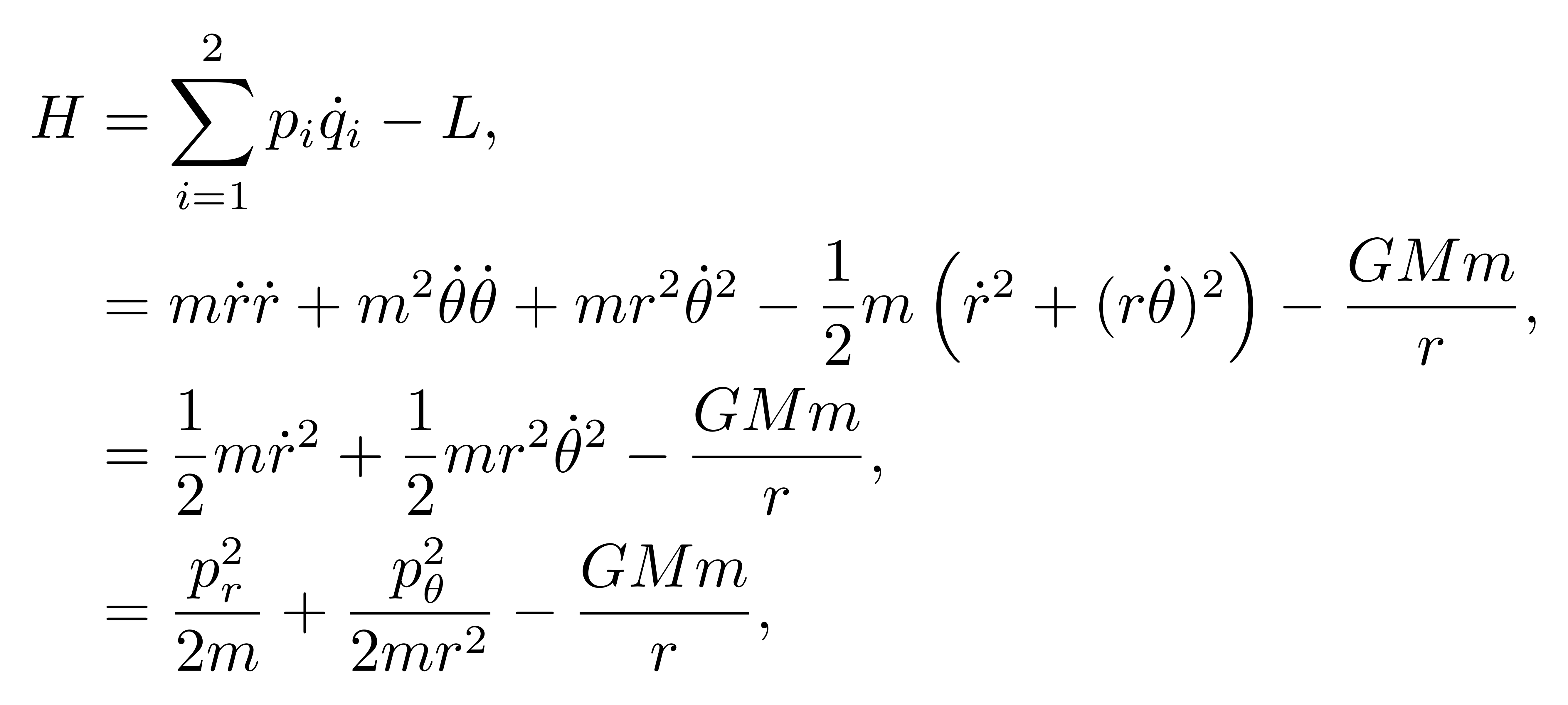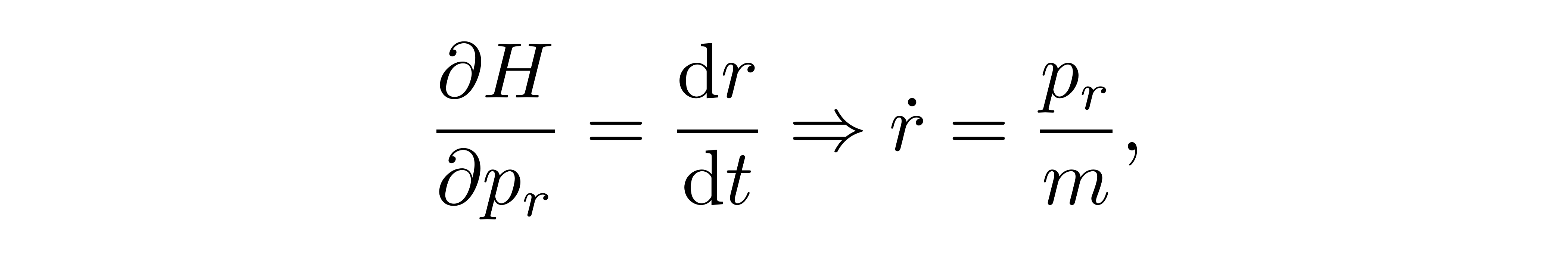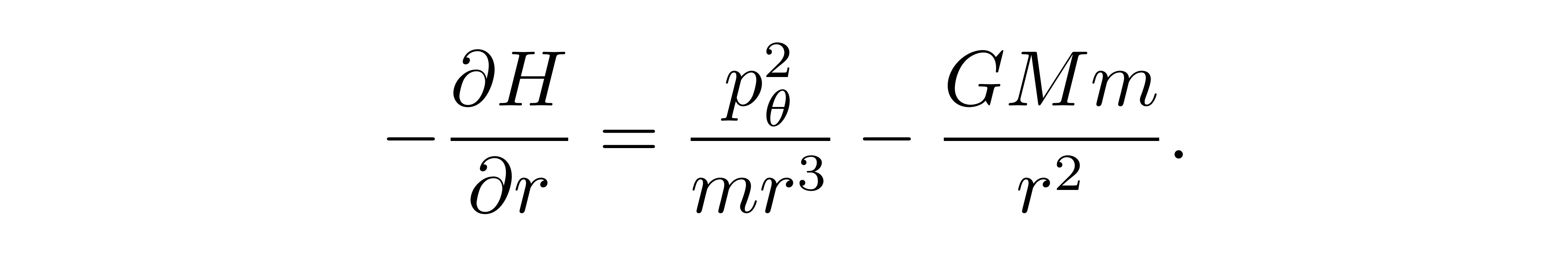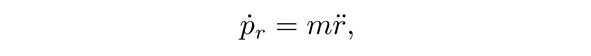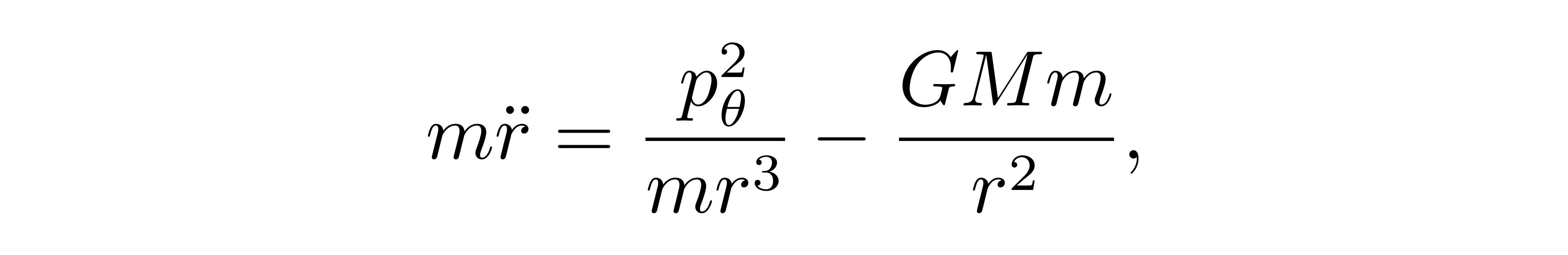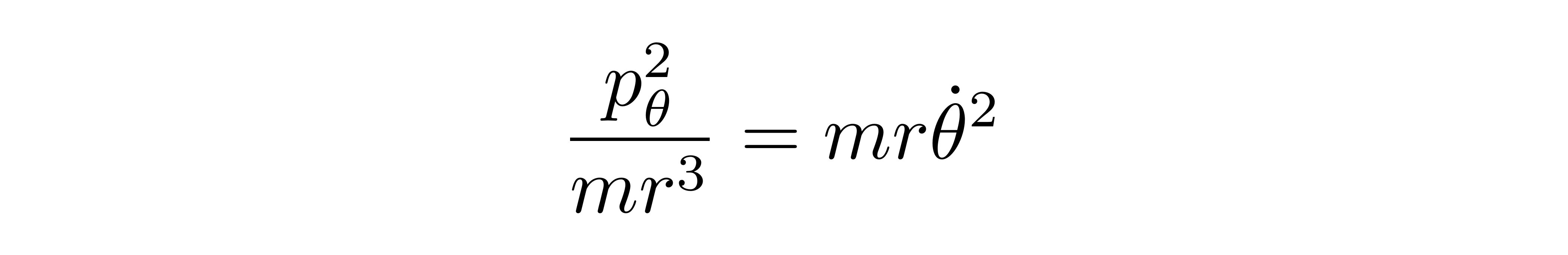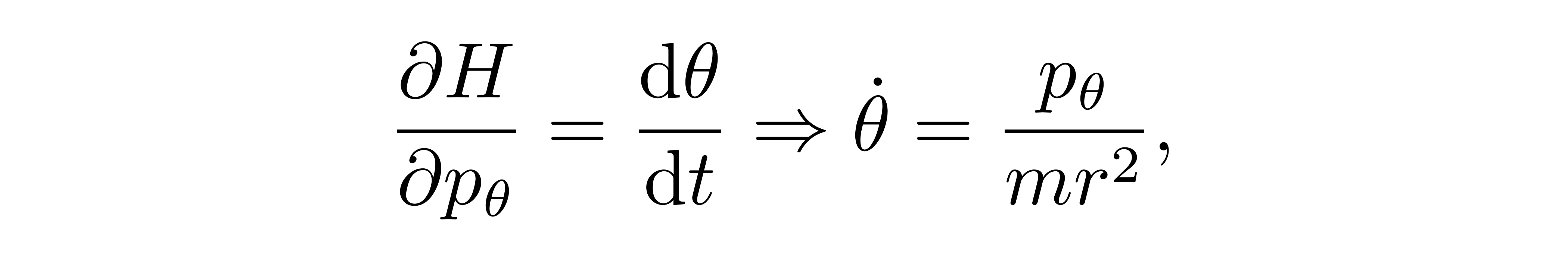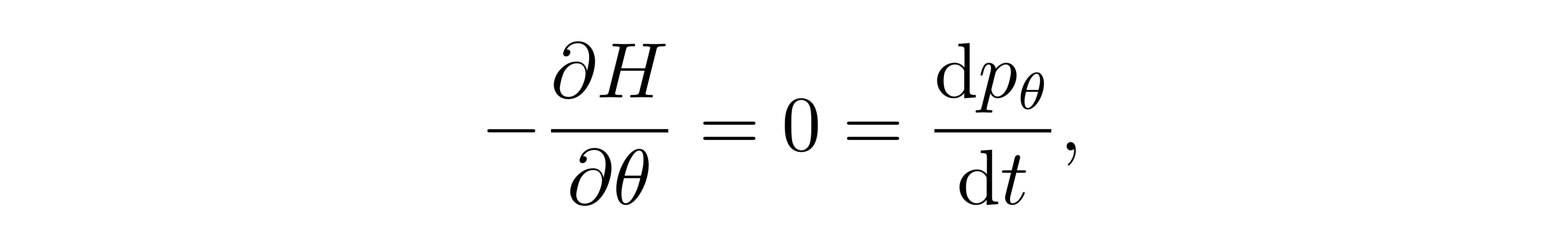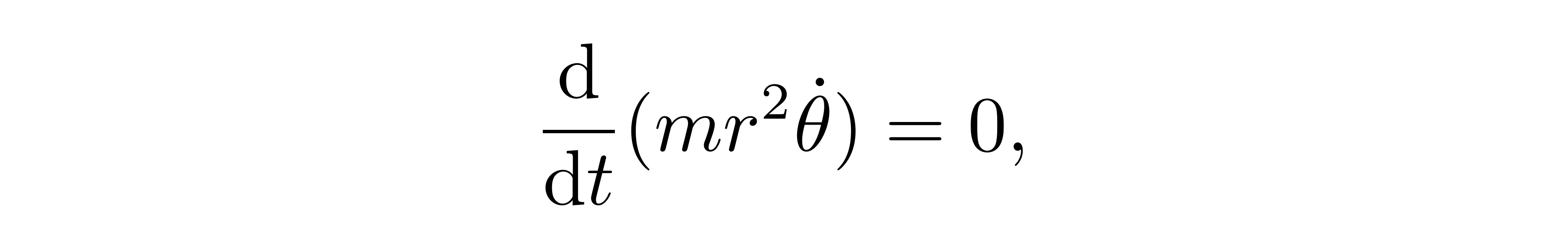On the plus side, the platform is available on mobile devices thanks to its mobile-friendly website.
Apart from the US, it also serves users from Canada, although players from Australia and UK are prohibited due to specific gambling laws.
What are the best hotels near Crown Casino in Melbourne? Some of the best hotels near Crown Casino in Melbourne are: Ink Hotel Melbourne Southbank - Traveler rating: 4.
5/5 Crown Towers Melbourne - Traveler rating: 4.
online casino florida The Golden Moon Hotel and Casino and the Bok Homa Casino, both under the Pearl River Resort umbrella, now have sports betting lounges.
During the calendar year for 2019 that number rose to $370 million.
从拉格朗日力学到哈密顿力学
自牛顿在17世纪建立起以矢量与几何关系为基础的力学框架后,因其泛用性和可靠性吸引了无数物理学家甚至数学家取深入阐发其内涵。在18、19世纪之交,由法国数学家拉格朗日(Lagrange)和德国数学家雅可比(Jacobi)等人率先发起了力学数学化表达的运动,用分析和代数方法重新构建了一套不同于矢量力学(牛顿力学),但又相互包容的框架,现代又被称之为“分析力学”。
在近几节直播课上,张朝阳以后一个角度,重新回归对经典力学的演算。他介绍道,拉格朗日提出,一个力学系统可以用一个称为拉格朗日量(Lagrangian)的函数来描述,它是广义坐标 q 及其对时间求导的函数
![]()
对经典的保守系统,它有相当简单的形式
![]()
即动能减去势能。系统的运动路径要求满足使得作用量最小的欧拉-拉格朗日方程
![]()
这里需要强调的是,在求偏导运算中,需要将拉格朗日量视为一个二元函数。此时,它的两个变量之间被视为是相互独立的——尽管物理上它们只要相差一个求导,即在求其中一个变量求导时,一般假设摁住另一个变量令其不再改变。为了强调这一点,再本节叙述中可以引入记号
![]()
以下标显式注明不变量。
注意到拉格朗日量中两个变量的不对称性,在拉格朗日力学发表的50年后,爱尔兰数学家哈密顿提出另一个现代被称为“哈密顿力学”的框架。哈密顿认为,力学系统可以用另一个被称为哈密顿量(Hamiltonian)的二元函数
![]()
表达。此时,它依赖的两个变量广义坐标 q 与广义动量 p,在物理意义上也相互独立,使得表达形式在数学上更为对称。在拉格朗日力学的基础上,哈密顿将广义动量定义为
![]()
而哈密顿量为
![]()
值得注意的是,此时等号坐标是 p 和 q 的函数,等号右边应当也保持一致。在实际推导时,应该将广义坐标的时间倒数连同拉格朗日量用新变量重新表达为
![]()
这一点在后面进行具体计算时尤为重要。现在考虑对哈密顿量求偏导,利用链式法则,
![]()
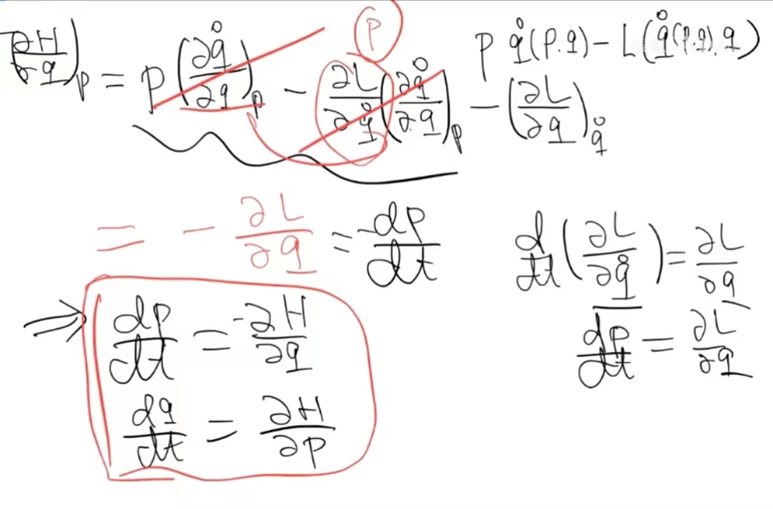
利用广义动量 p 的定义,不难看出,等号右边后两项可以互相抵消。于是有
![]()
类似地,可以求哈密顿量对广义坐标 q 的偏导数,有
![]()
再利用拉格朗日方程,最后一个等号可以继续化简为
![]()
两式结合,即得到哈密顿方程(组)
![]()
第二条等式中,等号左边是动量对时间的偏导,等号右边事实上定义了所谓的“广义力”。更值得一说的是,他们之间有相当对称的形式:某一变量随时间的演化,应由哈密顿量对另一变量的偏导决定,可以再一次印证前述提到变量 p 和 q 之间的对称性。
进一步,如果哈密顿量不显含时——即它对时间的依赖完全来自于两个变量对时间的依赖——时,可以证明,哈密顿量是系统的守恒量。同样是利用链式求导法则,
![]()
其中,第二个等号即用到了哈密顿方程(组)。
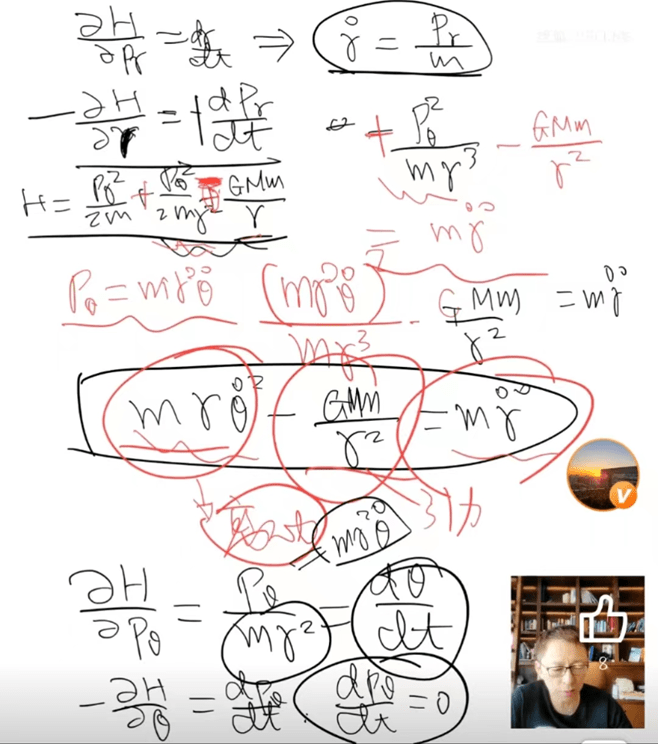
![]() (张朝阳推导哈密顿方程(组))
(张朝阳推导哈密顿方程(组))
利用哈密顿力学求天体运动方程
为了更好地理解哈密顿力学如何求解具体力学问题,不妨将其运用于考察中心力场,比如引力场中质点的运动。在前面的课程中,张朝阳曾演示过用拉格朗日力学来处理过这一问题。
![]()
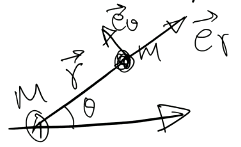
如图,假设有一个质量为 m 的天体微扰一个质量为 M 的天体转动。广义坐标仍取为径向距离 r 和角度 θ,体系的动能和势能分别可以写为
![]()
由于引力是保守力,拉格朗日量可以写为
![]()
对应的广义动量可以写为
![]()
反过来,广义坐标对时间的导数可以用广义动量表达为
![]()
于是,按定义哈密顿量应当取为
![]()
注意这里有多个广义坐标和对应的广义动量,在最后一步,需要把所有变量改写为以广义动量表达的形式。此时,求径向距离 r 和对应动量 pr 的哈密顿方程(组),首先
![]()
此即广义动量的定义式,并不带来新的内容。而对 r 求偏导,则有
![]()
等号另一边
![]()
于是可以得到
![]()
等号左边是加速度项,等号右边第二项是向内的引力,而第一项可以改写为
![]()
不难看出它即是向外的向心力,与用牛顿定理推出来的径向方程一致。再求角坐标 θ 相关的哈密顿方程(组),对广义动量求导
![]()
同样得到的是定义式。对应的另一条方程是
![]()
此即角动量守恒。更进一步,代入定义式
![]()
即得到开普勒定律。可以看到,哈密顿力学体系可以很容易地回到牛顿力学的结果。
![]() (张朝阳求解质点在中心力场中的运动方程)
(张朝阳求解质点在中心力场中的运动方程)
据了解,《张朝阳的物理课》于每周五,周日中午12时在搜狐视频直播,网友可以在搜狐视频APP“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。
online bet on cricketnevada online sports bettingonline real casino
声明:该文观点仅代表作者本人,搜狐号系信息发布平台,搜狐仅提供信息存储空间服务。