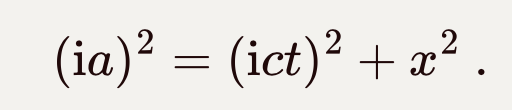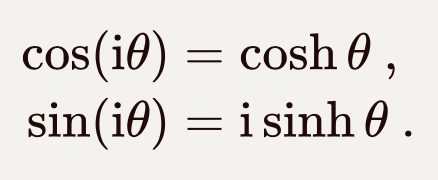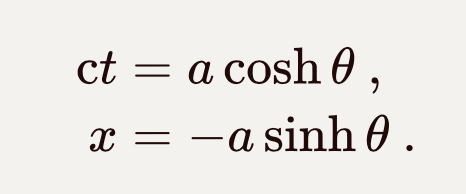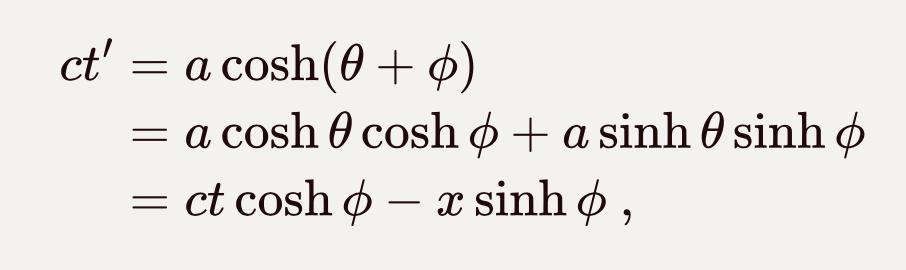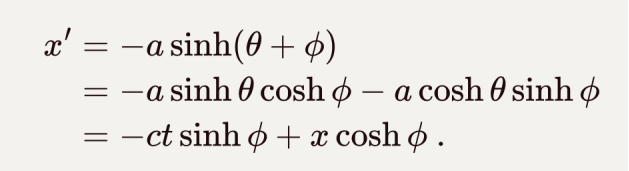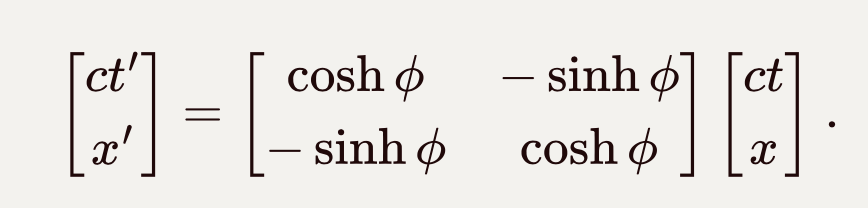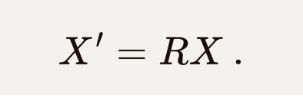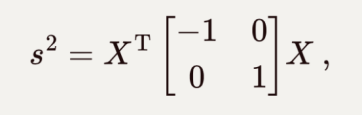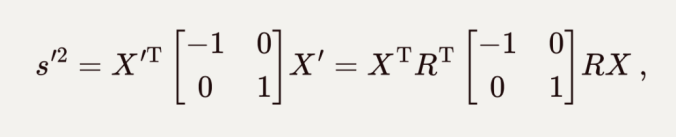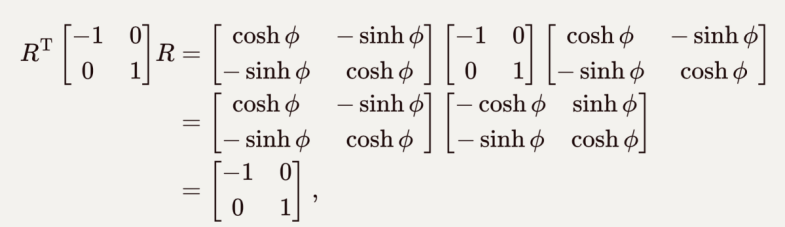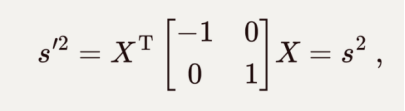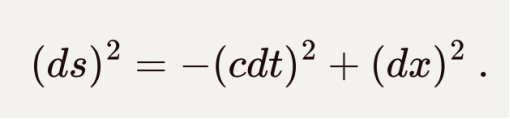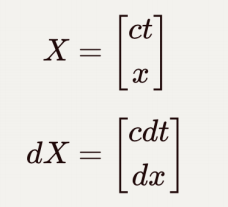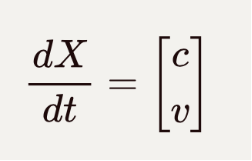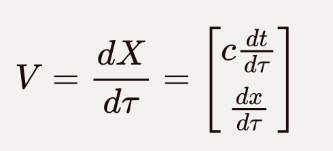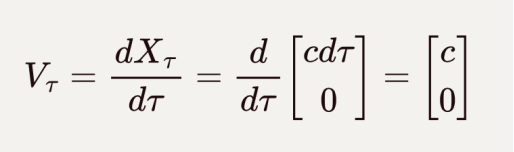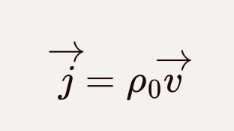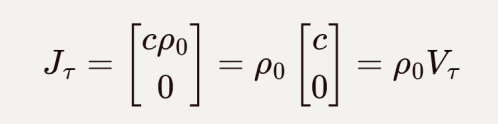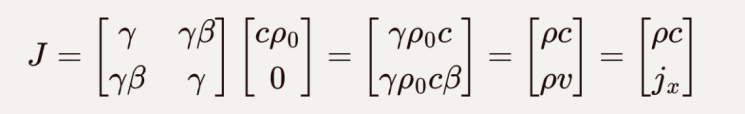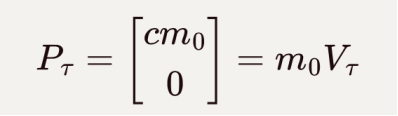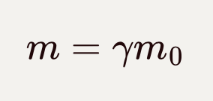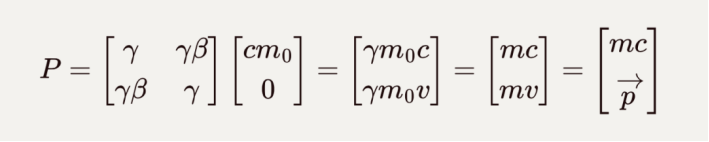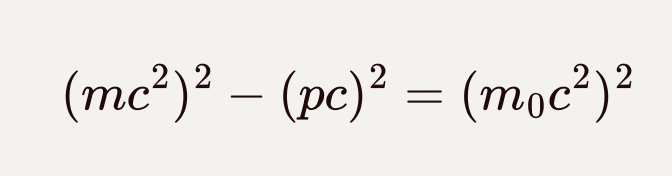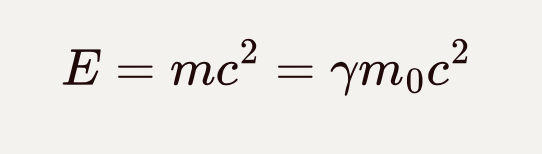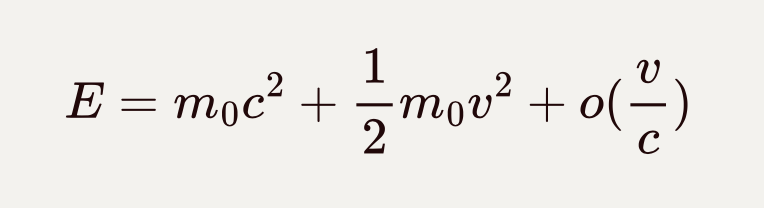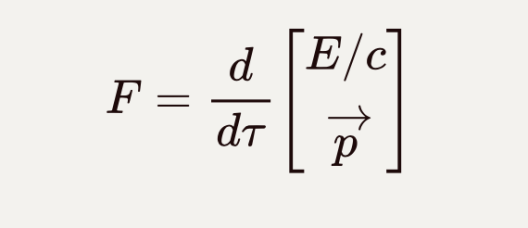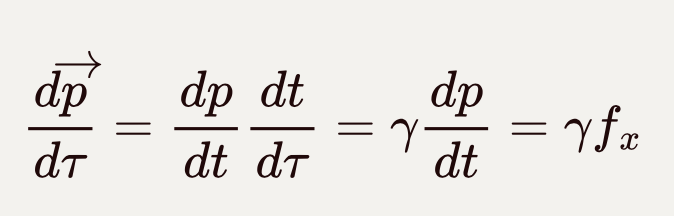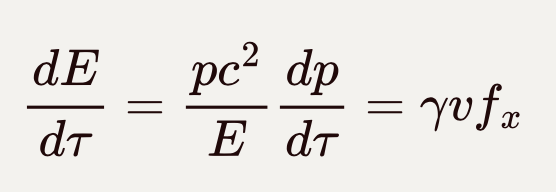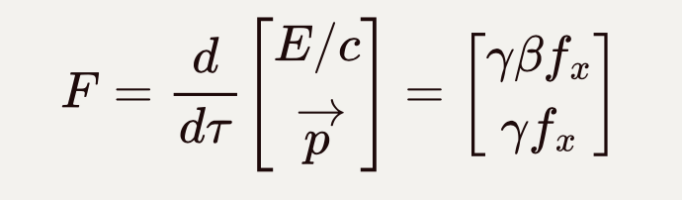ライブカジノゲームにおいて類まれなるディーラーコンテンツと安定したサーバー環境でのスムーズなゲームプレイを提供しているEzugi社は,地元の大手宝くじ会社Sisalと契約を結び,イタリア市場での活動をこれまでに以上の強化を図ることにしました.
また,近年,周辺市場や世界中でライブディーラーゲームの人気も爆発しています.
While the London home has acquired fame thanks to the iconic tartan motif of its products, it is also true that since 2000 there have been several image changes, involving Burberry shoes and bags.
Burberry therefore continues to establish itself as a fashion house appreciated and followed by both female and male audiences of any age.
easiest sport to bet on 6.
They also look really nice.

回顾洛伦兹变换与时空间隔
上一节张朝阳将时空间隔写成了空间坐标平方减去时间平方的二次型,如果用矩阵的方式来写,可以把时间前面的负号提出来:

时空坐标中间夹着的矩阵称为度规。s的平方是一个负数,这说明s是一个虚数,引入虚数单位i,记s的虚部为a,有:
![]()
这个形式的时空间隔长得就很像欧几里得空间的矢量长度了,也就具有相似的几何含义,可以视为闵氏空间上的“转动”。数学上有双曲函数:
![]()
可以将转动的角度变成一个虚数参量,θ→iθ,将三角函数换成双曲函数:
![]()
这里的θ相当于假想的转动角的虚部。如果在此基础上把时空坐标(ct,x)再伪转动一个参量φ,变成另一个时空坐标(ct’,x’)。根据双曲函数的运算规则,新的时空坐标是:
![]()
![]()
新旧坐标的变换可以用矩阵形式写成:
![]()
将其中的变换矩阵记为R,时空坐标记为X,可以简写为:
![]()
之前的推导都建立在时空间隔是不变量的基础上,反过来,也可以验证伪转动下时空间隔是保持不变的。原始的时空间隔是:
![]()
经过伪转动后:
![]()
其中:
![]()
所以,伪转动后时空间隔依然是:
![]()
由此验证了时空间隔在伪转动变换前后保持不变。
![]() 张朝阳讲解洛伦兹变换
张朝阳讲解洛伦兹变换
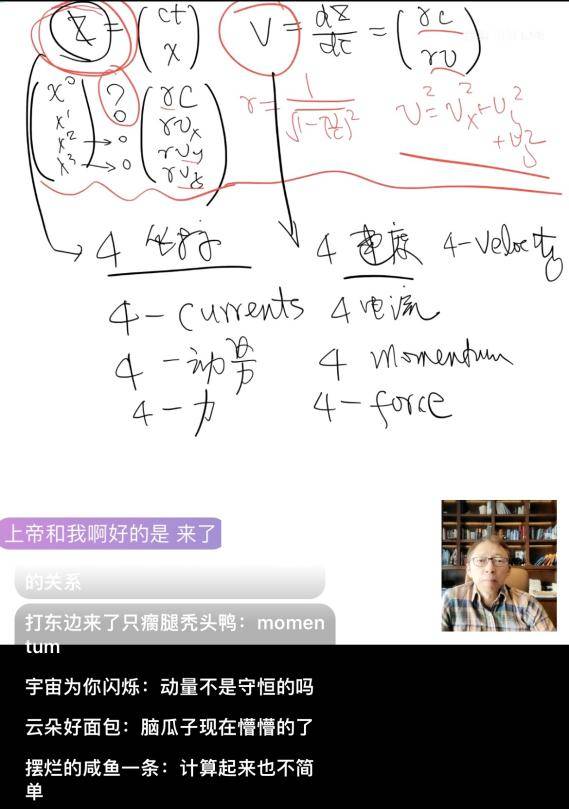
4维矢量的定义
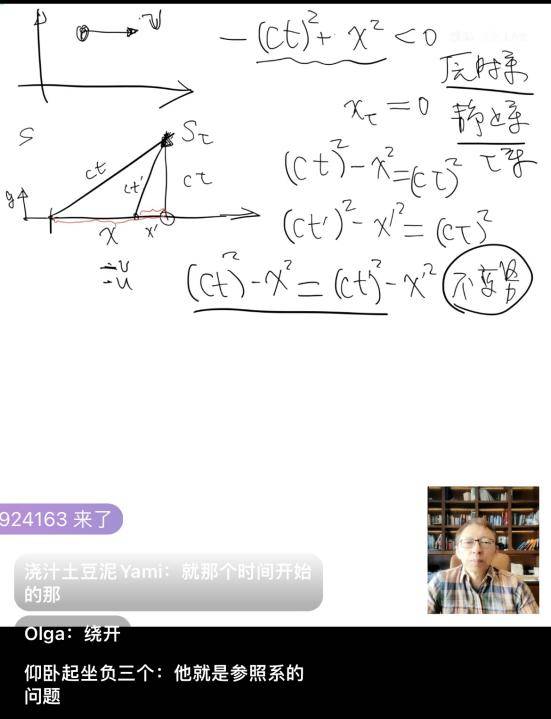
张朝阳在这里展示了一种几何的方式来直观理解各种四维矢量。首先,在两个在x方向相对匀速运动的参照系看一束光在x方向行驶,(ct)² - x² 都等于零,这提醒我们,即使粒子在x方向不以光速行驶,(ct)² - x²也可能是个不变量。可以通过如下思考来证明这一点。假定粒子以v速度在x方向行进, 在t =0时,在粒子静止的参照系(张朝阳形象的称这个参考系为“佛系”、“躺平系”),同时向y方向发出一束光,在t时刻,在“躺平系”,经历了τ时,在y方向走了cτ的高度撞到了光的接受器,在水平方向移动为零,假设y方向的高度不随水平方向运动的坐标系变换的影响(这是非常自然的假定),在S系看来,ct, x, cτ构成一个弦勾股直角三角形。而在相对于S系在水平方向匀速运动的S’系看来,y方向光的发出与接收两个事件在原时τ系走的高度也是cτ, 所以,ct’, x’, cτ也构成了弦勾股直角三角形,所以,(ct)² - x² = (ct’)² - x’² 是个不变量。如图所示:
![]() 张朝阳讲解“三角形规则”
张朝阳讲解“三角形规则”
使用这样的方法可以直观的理解各种4维矢量,比如四维位置矢量、四维速度等。三维位置矢量不再是不变量,需要将时间也一起考虑进去,变成“时空间隔”,即:
![]()
可以定义如下的四维位置矢量及位置矢量的微分:
![]()
但是此时位置矢量相对坐标时t的导数:
![]()
虽然具有速度的含义,但它的模长却不是一个四维不变量,真正的四维速度应该是:
![]()
在“躺平系”(共动坐标系)下的四维速度为:
![]()
经过检验,这样定义的四维位置矢量正是在洛伦兹变换下不变的量。
仿照这样的逻辑可以定义更多的四维矢量,例如四维电流J。
三维空间中的电流密度为:
![]()
其中在“躺平系”下的电荷密度为rho0,这时就可以定义“躺平系”下四电流为:
![]()
那么在相对运动的参考系下,由于电荷守恒以及长度收缩效应,电荷密度就变为:
![]()
由洛伦兹变换可以得到相应的四维电流密度为:
![]()
完全类似的,在“躺平系”下的“佛系”质量为m0,定义四维动量:
![]()
那么在相对运动的参考系下,质量为:
![]()
由洛伦兹变换可以得到相应的四维动量为:
![]()
由模长的关系可得:
![]()
令:
![]()
可以在低速下对E展开,有:
![]()
前两项正是静止质量对应的能量及动能。这说明相对论色散关系正来自于这样一种洛伦兹不变的四维动量。
最后可以定义四维力。方法完全类似四维速度来自于四维位置矢量对固有时的导数,再将四维动量对固有时求一次导数即可得到四维力:
![]()
其中空间分量为:
![]()
有力的量纲。而时间分量为:
![]()
具有功率的量纲。合起来得到四维力:
![]()
![]() 张朝阳讲解几种四维矢量
张朝阳讲解几种四维矢量
这里只考虑了沿x方向的情况,当然不失一般性。
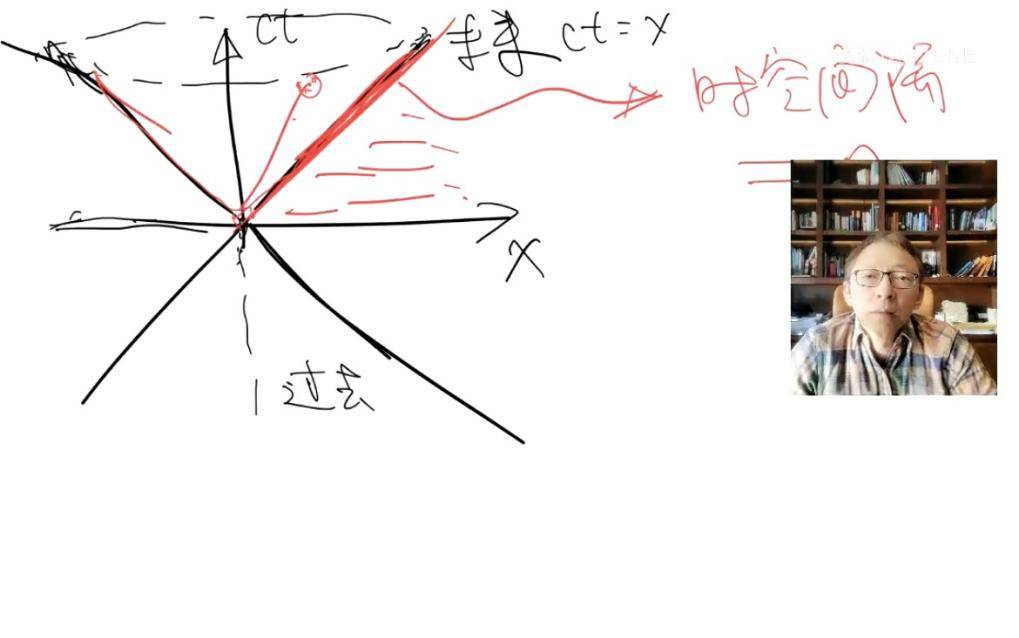
最后张朝阳讲解了什么是允许的物理运动,即在光锥中类时区域的运动,类空的则是被禁止的,分界线就是时空间隔为0的类光线。
![]() 张朝阳讲解光锥
张朝阳讲解光锥
nfl betting onlinecasino online pamlb online betting
声明:该文观点仅代表作者本人,搜狐号系信息发布平台,搜狐仅提供信息存储空间服务。